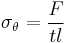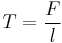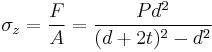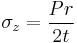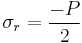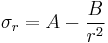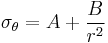Cylinder stresses

Circumferential stress is a type of mechanical stress of a cylindrically shaped part as a result of internal or external pressure.

The classic example of circumferential stress is the tension applied to the iron bands, or hoops, of a wooden barrel. In a straight, closed pipe, any force applied to the cylindrical pipe wall by a pressure differential will ultimately give rise to hoop stresses. Similarly, if this pipe has flat end caps, any force applied to them by static pressure will induce a perpendicular axial stress on the same pipe wall. Thin sections often have negligibly small radial stress, but accurate models of thicker-walled cylindrical shells require such stresses to be taken into account.

1 Definitions
2 Relation to internal pressure
- 2.1 Thin-walled assumption
- 2.2 Thick-walled vessels
3 Practical effects
- 3.1 Engineering
- 3.2 Medicine
4 Historical development of the theory
5 References

Definitions

One such type of stress is the hoop stress, which is defined for rotationally-symmetric objects as the average force exerted circumferentially (perpendicular both to the axis and to the radius of the object) in both directions on every particle in the cylinder wall. It can be described as:

$\sigma_\theta = \dfrac{F}{tl} \$

where:

F is the force exerted circumferentially on an area of the cylinder wall that has the following two lengths as sides:
t is the radial thickness of the cylinder
l is the axial length of the cylinder

An alternative to hoop stress in describing circumferential stress is wall stress or wall tension (T), which usually is defined as the total circumferential force exerted along the entire radial thickness:^[1]

$T = \dfrac{F}{l} \$

Along with axial stress and radial stress, circumferential stress is a component of the stress tensor in cylindrical coordinates.

It is usually useful to decompose any force applied to an object with rotational symmetry into components parallel to the cylindrical coordinates r, z, and θ. These components of force induce corresponding stresses: radial stress, axial stress and hoop stress, respectively.

Relation to internal pressure

Thin-walled assumption

For the thin-walled assumption to be valid the vessel must have a wall thickness of no more than about one-tenth (often cited as one twentieth) of its radius. This allows for treating the wall as a surface, and subsequently using the Young–Laplace equation for estimating the hoop stress created by an internal pressure on a thin wall cylindrical pressure vessel:

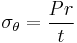$\sigma_\theta = \dfrac{Pr}{t} \$ (for a cylinder)

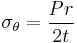$\sigma_\theta = \dfrac{Pr}{2t} \$ (for a sphere)

where

P is the internal pressure
t is the wall thickness
r is the inside radius of the cylinder.
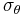$\sigma_\theta \!$ is the hoop stress.

The hoop stress equation for thin shells is also approximately valid for spherical vessels, including plant cells and bacteria in which the internal turgor pressure may reach several atmospheres.

Inch-pound-second system (IPS) units for P are pounds-force per square inch (psi). Units for t, and d are inches (in). SI units for P are pascals (Pa), while t and d=2r are in meters (m).

When the vessel has closed ends the internal pressure acts on them to develop a force along the axis of the cylinder. This is known as the axial stress and is usually less than the hoop stress.

$\sigma_z = \dfrac{F}{A} = \dfrac{Pd^2}{(d%2B2t)^2 - d^2} \$

Though this may be approximated to

$\sigma_z = \dfrac{Pr}{2t} \$

Also in this situation a radial stress 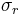$\sigma_r \$ is developed and may be estimated in thin walled cylinders as:

$\sigma_r = \dfrac{-P}{2} \$

Thick-walled vessels

When the cylinder to be studied has a r/t ratio of less than 10 (often cited as 20) the thin-walled cylinder equations no longer hold since stresses vary significantly between inside and outside surfaces and shear stress through the cross section can no longer be neglected.

In order to calculate the stresses and strains here a set of equations known as the Lamé equations must be used.

$\sigma_r = A - \dfrac{B}{r^2} \$

$\sigma_\theta = A %2B \dfrac{B}{r^2} \$

where

A and B are constants of integration, which may be discovered from the boundary conditions
r is the radius at the point of interest (e.g. at the inside or outside walls)

A and B may be found by inspection of the boundary conditions. For example, the simplest case is a solid cylinder:

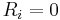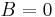if $R_i = 0$ then $B = 0$ and a solid cylinder cannot have an internal pressure so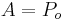 $A = P_o$

Practical effects

Engineering

Fracture is governed by the hoop stress in the absence of other external loads since it is the largest principal stress. Note that since the hoop stress is largest when r is smallest, cracks in pipes should theoretically start from inside the pipe. This is why pipe inspections after earthquakes usually involve sending a camera inside a pipe to inspect for cracks. Yielding is governed by an equivalent stress that includes hoop stress and the longitudinal or radial stress when present.

Medicine

In the pathology of vascular or gastrointestinal walls, the wall tension represents the muscular tension on the wall of the vessel. As a result of the Law of Laplace, if an aneurysm forms in a blood vessel wall, the radius of the vessel has increased. This means that the inward force on the vessel decreases, and therefore the aneurysm will continue to expand until it ruptures. A similar logic applies to the formation of diverticuli in the gut.^[2]

Historical development of the theory

The first theoretical analysis of the stress in cylinders was developed by the mid-19th century engineer William Fairbairn, assisted by his mathematical analyst Eaton Hodgkinson. Their first interest was in studying the design and failures of steam boilers.^[3] Early on Fairbairn realised that the hoop stress was twice the longitudinal stress, an important factor in the assembly of boiler shells from rolled sheets joined by riveting. Later work was applied to bridge building, and the invention of the box girder. In the Chepstow Railway Bridge, the cast iron pillars are strengthened by obvious bands of wrought iron. The vertical, longitudinal force is a compressive force, which cast iron is well able to resist. The hoop stress though is tensile, and so wrought iron, a material with better tensile strength is added.

References

^ Tension in Arterial Walls By R Nave. Department of Physics and Astronomy, Georgia State University. Retrieved June 2011
^ E. Goljan, Pathology, 2nd ed. Mosby Elsevier, Rapid Review Series.
^ Fairbairn, William (1851). Two Lectures: The Construction of Boilers, and On Boiler Explosions, with the means of prevention. p. 6. http://books.google.co.uk/books?id=VD5MAAAAMAAJ&ots=5RGGXukH7f&dq=fairbairn%20boiler&pg=PA6#v=onepage&q=hoop&f=false.

Thin-walled Pressure Vessels. 19 June 2008. http://www.efunda.com/formulae/solid_mechanics/mat_mechanics/pressure_vessel.cfm.